목차
- 분할 정복의 원리
- 이진 탐색
- 퀵 정렬
분할 정복의 원리
분할 정복은 순환적으로 문제를 푸는 하향식 방법입니다.
- 분할 : 주어진 문제 (입력)를 여러 개의 문제로 작게 분할.
- 정복 : 분할된 작은 문제들을 순환적으로 더 이상 분할되지 않을 때까지 분할, 충분히 작다면 순환 분할을 멈추고 그 문제의 해를 구함
- 결합 : 작은 문제들에서 정복한 해를 결합하여 원래 문제 (입력)의 해를 구함.
이 때 분할된 작은 문제들은 원래의 문제와 입력의 크기만 다를 뿐 동일합니다. 또한 각 문제들은 서로에게 독립적입니다.
분할 정복 알고리즘의 종류
- 이진 탐색
- 합병 정렬
- 퀵 정렬
- 선택 문제
이진 탐색
정렬되어있는 배열 (입력 데이터)에서 특정 값을 찾는 탐색 방법입니다. 이 때 찾으려는 값을 탐색키라고 합니다.
순서
- 분할 : 배열 (입력 데이터)의 가운데 원소를 기준으로 왼쪽, 오른쪽으로 분할. (탐색키와 가운데 원소가 같을 시, 가운데 인덱스를 반환 & 종료
- 정복 : 탐색키가 가운데 원소보다 작을 시 왼쪽부분 배열을 순환 호출, 가운데원소보다 클 시 오른쪽 부분배열을 순환 호출
결합 : 없음
구현
package main.java.com.study;
public class GandC {
public static void main(String[] args) throws Exception {
int[] items = {1, 4, 66, 123, 126, 130, 200, 201, 302};
int targetValue = 66;
System.out.println("찾으려는 값 : " + targetValue);
int idx = binarySearch(targetValue, items);
System.out.println("결과 인덱스 : " + idx);
}
//이진탐색
private static int binarySearch(int targetValue, int[] targetArray) {
int idxBegin = 0;
int idxEnd = targetArray.length + 1;
int resultValue = -1;
/*
* 값을 찾았는지 여부
* true : 값을 찾음 (반복문 멈춤)
* false : 값을 못 찾음 (반복문 지속)
* */
Boolean notFind = true;
while (notFind) {
int idxCenter = (idxBegin + idxEnd) / 2;
// 탐색키보다 작으면 -> 오른쪽 배열을 호출
if (targetArray[idxCenter] < targetValue) {
idxBegin = idxCenter + 1;
}
// 탐색키보다 크면 -> 왼쪽 배열을 호출
else if (targetArray[idxCenter] > targetValue) {
idxEnd = idxCenter - 1;
}
//선택한 값이 같으면 종료
else {
resultValue = idxCenter;
notFind = false; //값을 찾음 -> 멈춰
}
}
return resultValue;
}
}
퀵 정렬
배열의 원소를 오름차순 (혹은 내림차순)으로 정렬하는 방법입니다. 배열 중에 특정 기준으로 피벗이라는 값을 선택하여 정렬을 진행합니다. 피벗은 보통 다음 중 하나를 기준으로 정하여 진행합니다.
- 부분 배열의 가장 왼쪽 값
- 부분배열의 가장 오른쪽 값
- 부분배열의 가운데 값
순서
정복: 피벗을 정하여 해당 피벗이 제자리에 위치하도록 한다.
- index R은 부분배열의 오른쪽에서 출발해서 PVIOT보다 같거나 작은 값을 찾을 때까지, 왼쪽으로 이동. (원소 L보다 클 때까지만)
- index L은 부분 배열의 왼쪽에서부터 출발해서 PIVOT 보다 큰 값을 찾을 때까지 오른쪽으로 이동. (원소 R보다 작을 때까지만)
- 각자 멈춘 자리에서 L과 R을 서로 맞바꿈.
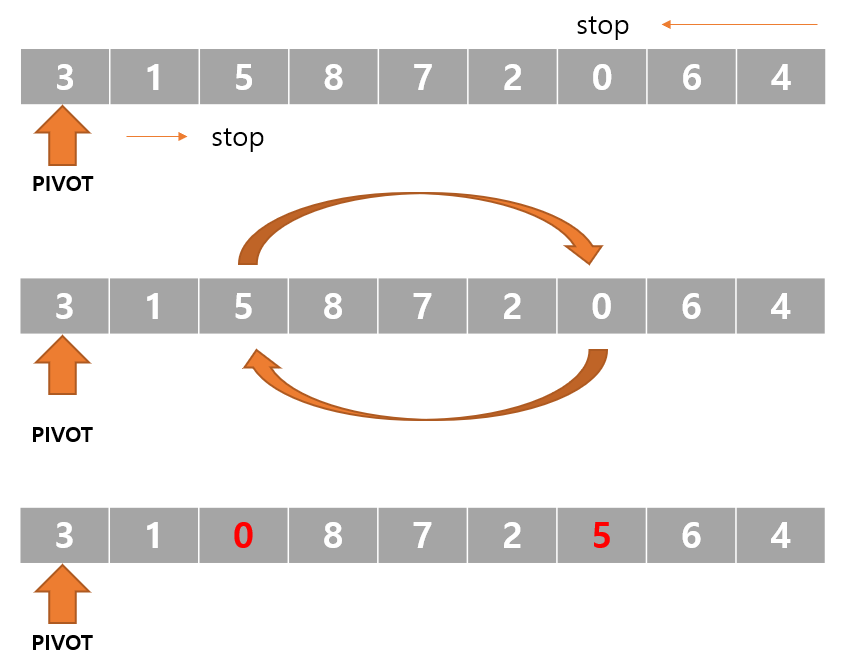
L이 R 보다 왼쪽에 있으면 위 과정을 반복. (재귀)
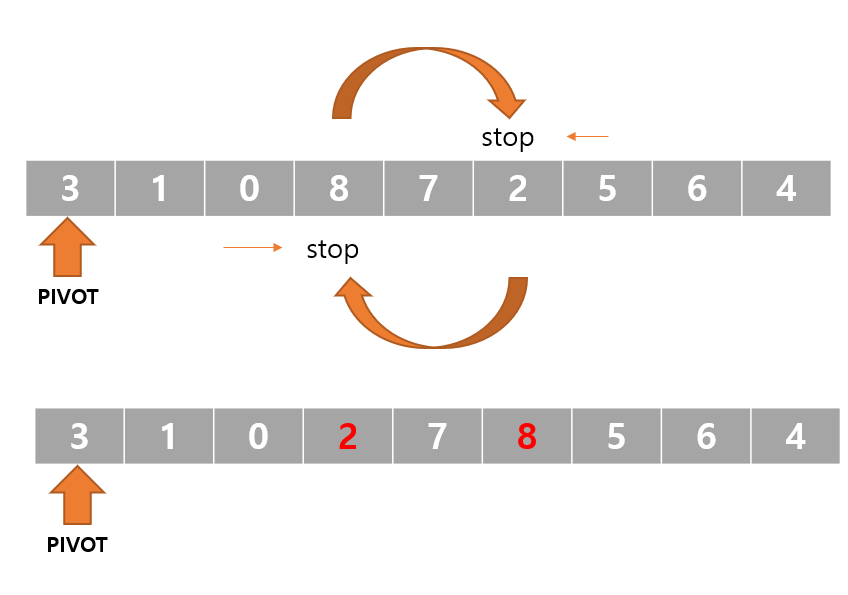
L과 R이 같은자리에 오게 되면 피벗과 L을 맞바꿈

이렇게 피벗을 기준으로 한 번의 작업이 끝나면 피벗을 기준으로 왼쪽에는 피벗보다 작은 값이, 오른쪽에는 피벗보다 큰 값들이 위치합니다.
분할 : 제자리에 위치한 피벗을 기준으로 왼쪽 / 오른쪽 부분 배열로 나누어 다시 정복을 순환함
3. 결합 : 없음
피벗을 제자리에 위치하도록 하는 작업을 각 부분 배열 별로 반복해서 진행하면 결국 모든 원소가 자기 자리에 위치하게 되어 정렬되는 알고리즘입니다.
구현
package main.java.com.study;
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) throws Exception {
// int[] items = {8, 1, 5, 2, 7, 3, 0, 6, 4}; //최악의 경우
int[] items = {3, 1, 5, 8, 7, 2, 0, 6, 4};
System.out.println("정렬 전 : " + Arrays.toString(items));
quickSort(items, 0, items.length - 1);
System.out.println("정렬 후 : " + Arrays.toString(items));
}
private static void quickSort(int[] items, int idxL, int idxR) {
// 정렬할 부분배열의 길이가 1 이상일경우에만 진행
if (idxL < idxR) {
int idxPivotAfterPartition = partition(items, idxL, idxR);
//Left array
quickSort(items, idxL, idxPivotAfterPartition - 1);
//Right array
quickSort(items, idxPivotAfterPartition + 1, idxR);
}
}
//파티션 : 피벗을 제자리에 위치시킴
private static int partition(int[] items, int idxL, int idxR) {
int idxPivot = idxL;
while (idxL < idxR) {
while (idxL < idxR && items[idxPivot] < items[idxR]) {
idxR--;
}
while (idxL < idxR && items[idxL] <= items[idxPivot]) {
idxL++;
}
swap(items, idxL, idxR);
}
swap(items, idxL, idxPivot);
return idxL;
}
private static void swap(int[] items, int idx1, int idx2) {
int temp = items[idx1];
items[idx1] = items[idx2];
items[idx2] = temp;
}
}
'Programming > Languages (Java, etc)' 카테고리의 다른 글
| JSP란 (0) | 2022.10.05 |
|---|---|
| JAVA는 call by reference 없습니다. (0) | 2022.07.19 |
| 싱글톤 패턴 (Singleton pattern) (0) | 2022.05.10 |
| 알고리즘의 기본 - 시간복잡도 (0) | 2022.03.18 |
| 알고리즘을 공부하기 위한 기초지식 - 자료구조 (0) | 2022.03.11 |




댓글